##一. 基础
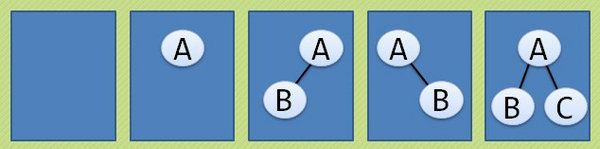
▲ 二叉树有5种基本形态
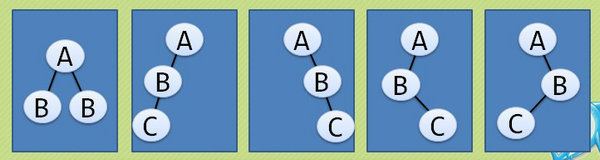
▲ 三个节点的普通二叉树有5种形态
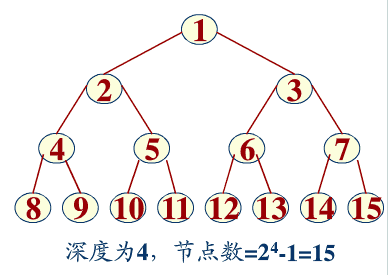
▲ 深度为4的满二叉树
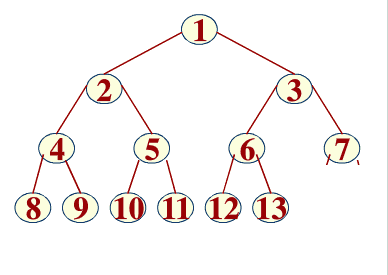
▲ 完全二叉树左子树满,右子树可能满可能不满
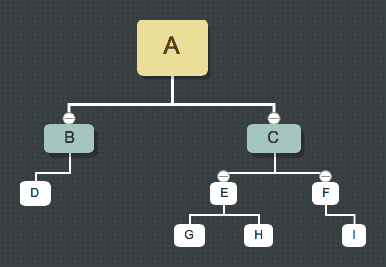
前序遍历(NLR)(根左右):A B D C E G H F I
中序遍历(LNR)(左根右):D B A G E H C F I
后序遍历(LRN)(左右根):D B G H E I F C A
层序遍历:A B C D E F G H I
##二. 递归 用代码实现二叉树有一种非常简便的方法,就是递归。那什么是递归呢?

呀!放错图片了(≧∇≦)有问题找Google!
Google 别闹!哈哈!
还是让我来给大家讲个故事吧!从前有座山,山上有座庙,庙里有个老和尚,老和尚对小和尚说:从前有座山,山上有座庙,庙里有个老和尚,老和尚对小和尚说:从前有座山,山上有座庙,庙里有个老和尚,老和尚对小和尚说……
上面这个故事只是描述了递,没有描述归。
小明问小红:今天星期几?
小红不知道。
小红问小芳:今天星期几?
小芳不知道。
小芳问小强:今天星期几?
小强对小芳说:星期天。
小芳对小红说:星期天。
小红对小明说:星期天。
小明说:哈哈,又可以出去玩了!
▲ 上面就是递归的例子,有递有归。
n! = n x (n-1) x (n-2) x ... x 1
令f(n) = n x f(n-1)
则f(n) = n x (n-1) x f(n-2)
则f(n) = n x (n-1) x (n-2) x f(n-3)
...
则f(n) = n x (n-1) x (n-2) x ... x 2 x f(1)
令f(1) = 1
则f(n) = n x (n-1) x (n-2) x ... x 2 x 1 = n!
▲ 计算阶乘,上面的f函数相当于今天星期几,f(1)=1是初始值,也即边界条件,相当于小强知道星期天,从f(n)算到f(1),然后再从f(1)的初始值依次返回,得到f(n)的值,这个实现过程很像栈,后进先出,f(1)是最后被调用但是最先返回。既然递归是用堆栈实现的,那就要留意递归的层数了,层数如果超出堆栈的最大长度,那估计就会堆栈溢出了,这也是递归要小心的地方。
public class test {
public static void main(String[] args){
for (int i = 1; i <= 10; i++) {
System.out.println(func(i));
}
}
public static int func(int n){
if(n == 1 || n == 2){
return 1;
}else{
return func(n-1)+func(n-2);
}
}
}
▲ 计算斐波那契数列,有很多类似斐波那契数列的题目都能用递归求解。兔子繁殖,第三个月开始生小兔子,小兔子第三个月又生小兔子…树枝生长问题,一年后长出一个树枝,这个树枝一年后变老,老树枝又长出新树枝…台阶问题,可以一次走两级或一级,走10级台阶有几种走法…蜜蜂路径问题…等等。
如果你还是不知道什么是递归,你可以看看这篇文章
##三. 二叉树实现 讲完递归,我们再回过头看看二叉树的代码实现。
二叉树由根节点,左子树和右子树构成,数据结构为lchild data rchild。lchild或rchild有可能为null。
class Node:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
▲ Python实现的二叉树数据机构
g = Node('G')
h = Node('H')
e = Node('E', g, h)
i = Node('I')
f = Node('F', None, i)
c = Node('C', e, f)
d = Node('D')
b = Node('B', d)
a = Node('A', b, c)
root = a
▲ 定义的时候从最底层开始,最后到根节点(就是上面图中的二叉树)
def VisitTree_Recursive(root, order):
if root:
if order == 'NLR': print(root.data)
VisitTree_Recursive(root.left, order)
if order == 'LNR': print(root.data)
VisitTree_Recursive(root.right, order)
if order == 'LRN': print(root.data)
▲ 二叉树的遍历实现,用到了递归,就短短几行代码实现了看似复杂的前序遍历、中序遍历和后序遍历,太神奇了!
对于前序遍历NLR,则是先访问根节点数据即print(root.data),再分别遍历左子树和右子树。
对于中序遍历LNR,则是先遍历左子树,遍历完左子树再打印节点数据,再遍历右子树。
对于后序遍历LRN,则是先遍历左子树和右子树,最后打印根节点数据。
public class test {
public static void main(String[] args){
node g = new node("G", null, null);
node h = new node("H", null, null);
node e = new node("E", g, h);
node i = new node("I", null, null);
node f = new node("F", null, i);
node c = new node("C", e, f);
node d = new node("D", null, null);
node b = new node("B", d, null);
node a = new node("A", b, c);
recurse(a, "LRN");
}
public static void recurse(node root, String order){
if(root != null){
if (order.equals("NLR")){
System.out.println(root.data);
}
recurse(root.lchild, order);
if (order.equals("LNR")){
System.out.println(root.data);
}
recurse(root.rchild, order);
if (order.equals("LRN")){
System.out.println(root.data);
}
}
}
}
class node{
String data;
node lchild;
node rchild;
public node(String data, node lchild, node rchild){
this.data = data;
this.lchild = lchild;
this.rchild = rchild;
}
}
▲ 用JAVA实现二叉树的数据结构和三种遍历
##四. 问题
-
求二叉树节点个数
public static int node_num(node root){ if(root == null){ return 0; } return node_num(root.lchild)+node_num(root.rchild)+1; }▲ 用递归计算的节点数,写的时候好别扭,运行之后是对的,关键点是左子树的节点数加上右子树的节点数加根节点1.
-
求二叉树深度
public static int getDepth(node root){ if(root == null){ return 0; } return getDepth(root.lchild) >= getDepth(root.rchild) ? getDepth(root.lchild) + 1 : getDepth(root.rchild) + 1; }▲ 用递归计算二叉树深度。边界条件:如果根节点为null返回0.否则返回左子树和右子树中的较大者加1.好抽象…写代码的时候我只能感觉是对的,然后运行是对的,有种很不确定的感觉…这里的1很玄奥!它是一个相对的概念。而上面return的0是一个绝对的值。通过“递”到一个绝对值0上然后通过依次加1“归”到最上层。
-
层序遍历
public static void levelOrder(node root){ Queue<node> queue = new LinkedList<node>(); queue.offer(root); while (!queue.isEmpty()){ node anode = queue.poll(); System.out.println(anode.data); if (anode.lchild != null) queue.offer(anode.lchild); if (anode.rchild != null) queue.offer(anode.rchild); } }▲ 这次没有用递归,不知道递归能不能实现。使用队列实现,遍历上一层的时候,将下一层从左往右压入队列。
-
获取第K层节点数和相应的数据
f(root,k) = f(root.lchild,k-1) + f(root.rchild,k-1) = f(node,1) + f(node,1) + ... + f(node,1) 边界条件1: f(node,k) = 0 <- node=null or k < 1 边界条件2: f(node,k) = 1 <- node!=null and k = 1 递归3: f(node,k) = f(node.lchild,k-1) + f(node.rchild,k-1) <- node!=null and k>1▲ 递归的公式以及边界条件,这样推导之后清楚很多。
public static int getLevelNum(node root,int k){ if (root == null || k < 1){ return 0; }else if(k == 1){ System.out.print(root.data); return 1; } return getLevelNum(root.lchild, k-1) + getLevelNum(root.rchild, k-1); }▲ 通过递归实现。
-
获取叶子节点数
public static int getLeaves(node root){ if(root == null){ return 0; }else if (root.lchild == null && root.rchild == null){ return 1; } return getLeaves(root.lchild) + getLeaves(root.rchild); }▲ 条件1:root为null则返回0,条件2:root的左孩子和右孩子同时为null,返回1,其他3:左孩子的叶子节点数加右孩子的叶子节点数。
-
非递归前序遍历
/** * 非递归前序遍历:进栈是前序遍历,出栈是中序遍历。 * @param root */ public static void printNLR(node root){ Stack<node> stack = new Stack<node>(); while (root != null || !stack.empty()){ if (root != null){ System.out.println(root.data); stack.push(root); root = root.lchild; }else { root = stack.pop(); root = root.rchild; } } }▲ 在使用非递归实现前序遍历的时候,使用栈来维护序列。入栈打印数据是前序遍历,出栈打印数据是中序遍历。持续访问左孩子,左孩子为空则出栈访问右孩子。
-
非递归中序遍历
public static void printLNR(node root){ Stack<node> stack = new Stack<node>(); while (root != null || !stack.empty()){ if(root != null){ stack.push(root); root = root.lchild; }else { root = stack.pop(); System.out.println(root.data); root = root.rchild; } } }▲ 原理同前序遍历
-
非递归后序遍历
public static void printLRN(node root){ Stack<node> stack = new Stack<node>(); node pre = null; while (root != null || !stack.empty()){ if (root != null){ stack.push(root); root = root.lchild; }else if (stack.peek().rchild != pre){ root = stack.peek().rchild; pre = null; }else { pre = stack.pop(); System.out.println(pre.data); } } }▲ 多了个辅助变量
pre来维护,采用左右根的顺序来访问,在弹出根节点之前还要访问右孩子。当前节点为null,且兄弟节点也为null或者已经访问过pre,则输出栈中数据。 -
最小公共祖先
public static node printLCA(node root, node n1, node n2){ Stack<node> stack = new Stack<node>(); Stack<node> s1 = new Stack<node>(); Stack<node> s2 = new Stack<node>(); node pre = null; while (root != null || !stack.empty()){ if (root != null){ stack.push(root); root = root.lchild; }else if (stack.peek().rchild != pre){ root = stack.peek().rchild; pre = null; }else { if(stack.peek() == n1){ s1 = (Stack<node>)stack.clone(); //这个栈属于引用传递,s1 = stack;会使s1指向stack }else if(stack.peek() == n2){ s2 = (Stack<node>)stack.clone(); } pre = stack.pop(); System.out.println(pre.data); } } while (!s2.empty()){ node lca = s2.pop(); if(s1.contains(lca)){ return lca; } } return null; }▲ 困扰了好久,网上有很多先进的算法解决方案,还用到了并查集,比如这个,算法太难理解了,所以我自己写了一个简单易懂的。采用的是非递归的后序遍历,这样遍历可以得到根节点到各个节点的分支路径,分别把想要的两个节点的分支路径缓存起来,用栈来维护,最后再从栈顶到栈底得到最小的公共节点。
##其他二叉树 ####1.二叉查找树 左子树小于根节点,右子树大于根节点。
####2.平衡二叉树 左右子树的深度差绝对值不超过1
####3.平衡查找树–2-3树 有2个或3个子树。一个节点包含一个值,则有两个子树,左子树比这个值小,右子树比这个值大。一个节点包含两个值,则有三个子树,左子树比最小的值小,中子树介于两个值之间,右子树比最大的值大。
####4.平衡查找树–红黑树 一种自平衡二叉查找树,用颜色的约束关系来保持最长路径不大于两倍的最短路径。1.节点非红即黑 2.根节点为黑色 3. 叶子都是黑色(nil节点) 4.每个红节点必须有两个黑色子节点(没有两个连续红节点) 5. 任一路径黑色节点数相同。有的时候会用红黑来描述当前节点连接父节点的链接颜色,实际是一样的,只不过可以更好的和2-3树联系起来。
####5.平衡查找树–B树 一个节点可以拥有多于2个子节点的二叉查找树,2-3树的扩展。
M阶B树满足以下条件:
- 每个节点至多有M棵子树,M-1个键值
- 除根节点外,其他每个分支节点至少有M/2棵子树
- 根节点至少有两棵子树(多于一个节点情况下)
- 所有叶子结点都在同一层上
- 有j棵子树的非叶子结点有j-1个关键码且递增排序
####6.平衡查找树–B+树 B+树相比于B树,内部节点(非叶子节点)只保存键值,不保存有效信息,用于索引,只包含子树根节点中的最大或最小键值。一个叶子节点包含一个指针,指向另一个叶子节点以加速顺序存取。
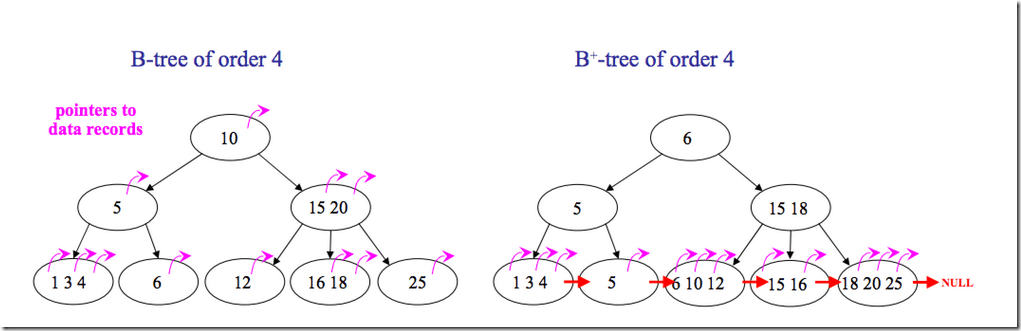
▲ B树和B+树的区别
##参考文献:

